Field Curvature

The focal planes of most telescopes are not flat. Off-axis light usually focuses closer to the objective than does on-axis light.

Above: A curved focal plane

For visual observing, a slightly curved field is no big deal. The eyepiece will compensate somewhat, and if the stars at the edge of the field are slightly out of focus compared to stars in the middle, the eye itself can accommodate to a certain extent. Severely curved fields would be problematic, but these are rare.

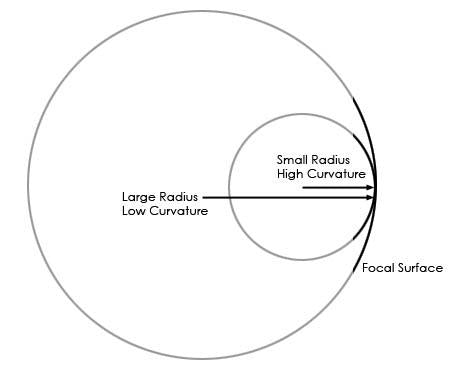
Field curvature is measured in terms of a radius of curvature. Since a curved field is a small section of a circle, the radius of that circle describes the amount of curvature (see below).

Above: A field with a large radius of curvature has little curvature (is relatively flat), and one with a small radius is highly curved

Field curvature becomes a problem, however, for photography. Since imaging detectors (CCDs, film, etc.) are normally flat, a curved focal plane cannot coincide exactly with the detector. In the past, some telescope designs incorporated a mechanism to curve film to match the curved focal plane. With most astronomers using CCDs and digital cameras now, this is no longer possible. A curved field only coincides with a flat detector at one off-axis distance (see diagram below).

Above: A curved focal plane and a flat imaging detector such as a CCD chip

Due to a telescope's inherent depth of focus, the region where the focal plane is in focus on the detector is larger than just the area where the focal plane coincides with the detector. (For more details on this, see the Guide to CCD Imaging page on Focusing.) As long as the field curvature is relatively small, it will not be too problematic. But for very large CCD chips and highly curved fields, it will be impossible to get small, sharp stars across the entire field.

It is possible to design a telescope with a flat focal plane, making it ideal for imaging. However, this usually complicates the design or requires a compromise in other regards, so usually some field curvature is tolerated, especially in multi-purpose telescopes. Also, some telescopes incorporate field-flatteners, to reduce the amount of field curvature when being used for photography.

Telescopes with Field Curvature

Most telescopes have curved focal planes. Refractors, Newtonians, and almost all common Cassegrain designs including Schmidt-Cassegrainsand Ritchey-Chrétiens have field curvature. In a standard Newtonian, field curvature is directly related to focal length. In fact, radius of field curvature is equal to focal length. So an 8" f/6 Newtonian has curved field with a radius of 1200mm, while an 8" f/4 has a field curvature radius of 800mm. Therefore the faster (f/4) telescope has greater field curvature (a more strongly curved field).

In more complex optical systems, there is often not a direct relationship between focal length or focal ratio and field curvature. This is because field curvature is closely related to astigmatism, and in optical systems with some residual astigmatism (including refractors and most Cassegrains), field curvature is partially determined by astigmatism. In general, though, with refractors, field curvature is still primarily related to focal length. Short refractors tend to have greater curvature than long refractors. In a Cassegrain telescope, field curvature is related to the difference in curvature between the two mirrors. If both mirrors have the same curvature, the field is flat (or nearly so, depending on astigmatism). Unfortunately, this leads to other difficulties in constructing the scope or to other optical compromises. For this reason, the common commercial SCTs, Maksutov-Cassegrains, and Ritchey-Chrétien's all have field curvature and require the use of a field flattener to produce a flat focal plane.

The table below shows a few common telescopes and the radii of curvature of their focal surfaces. The necessary depth of focus is given assuming the use of a large-format 35mm CCD chip (or DSLR, or what was that old grainy stuff...oh yeah, film). Notice that none of the telescopes listed provide a flat enough field to have the entire 35mm frame in focus at once. The 8" f/6 Newtonian and 8" f/4 Schmidt-Newtonian come close, but these designs suffer from enough coma that field curvature is the least of the concerns. Field flatteners and focal reducers will significantly decrease the required depth of focus. Also, if we take the depth of focus for seeing-limited resolution (which is more realistic for long-exposure imaging than the theoretical diffraction limit), the situation improves as well.

The diagram below shows the spot diagrams for an 80mm f/7.5 ED doublet refractor. The first set of spots shows the star sizes for a flat field. This is how the stars would be imaged by a CCD camera. (Note the field of view is for a 35mm-sized chip, which has a diagonal size of 42mm, hence 21mm off-axis is the corner of the field.) The second set of spot diagrams are for an idealized curved field. The radius of field curvature for such a scope is 220mm. Note that the stars become smaller when the ideal curved field is used. Of course, this is impossible to do in practice (since a CCD chip cannot be bent). It shows why a telescope designed to have a flat field is important. (Note also that the star images are still not perfect, even when the field is curved, since there are still other aberrations--mostly astigmatism--affecting the image.)

Above: Spot diagrams for an 80mm f/7.5 refractor. Spots on the left are for a flat field (the way a CCD camera would see the stars), while the spots on the right are for an ideal curved field. Spot diagrams generated using ATMOS software by Massimo Riccardi.

Telescopes without Field Curvature

Certain telescopes are specially designed to produce a flat focal plane. These are intended for photographic use as field curvature is not problematic for visual observation. Other telescopes incorporate an additional field flattener lens near the focal plane to create a flat field. This lens is often removed for visual work to reduce the number of lens elements in the telescope.

While typical doublet and triplet refractors suffer from field curvature, some refractors are designed to have flat fields. One well-known design for this purpose is called a Petzval design. The popular TeleVue NP-101 and Takahashi FSQ106 make use of this design. This design uses a doublet at the front of the telescope, and a second pair of lenses near the focuser to flatten the field and produce a fast focal ratio (around f/5). Other refractors add a field flattener as an accessory for photographic purposes.

It is possible to design a flat-field Schmidt-Cassegrain, but these are typically not compact designs and so are only occasionally seen among amateur telescope makers. Other popular Cassegrain designs such as Ritchey-Chrétiens often use field flatteners to eliminate the large amount of field curvature associated with the design.

Newtonians have less field curvature than many designs, but fast systems still have excessive curvature for wide-field photography. Highly modified Newtonian designs, such as Takahashi's Epsilon hyperbolic astrographs, use correcting lenses to produce very large flat fields.

Note: Some telescope manufacturers will show spot diagrams using an ideal curved field. This shows the optimum star images, but does not accurately represent what a camera would see. Curved-field spot diagrams are only useful for analyzing residual aberrations such as astigmatism. For real-world results, flat-field spot diagrams should always be used. In this case, only scopes with inherently flat fields, such as those listed above, will show small stars at the edge of the field.