Focusing

Why is focusing such an important aspect of CCD imaging? The following section describes the theory behind focus in telescope optics to give a deeper understanding of this critical procedure.

  How Telescopes Focus Light

Knowledge of how telescope optics focus light from a celestial object will aid in the understanding of accurately focusing a CCD image. Some of the tricky aspects of CCD focusing will become apparent.

  Simple Focus

To begin with, we'll take a simplified example. Imagine a lens which is designed to focus the light from distant stars. Starlight comes down from the sky in effectively parallel lines, strikes the glass in the lens, is refracted by the glass, and reaches a focus point somewhere behind the lens. This distance behind the lens is determined by the curvature of the lens and is called the focal length of the optic.

Above: A simplified lens focuses light from distant stars to a point behind the lens.

An eyepiece placed at this focus point will create an image which can be viewed. Placing a CCD chip at this point would allow the telescope image to be captured. If the camera is moved closer to the lens, the image appears out of focus because the light cone is still converging. Instead of pinpoints, the stars now appear as disks. These disks become larger the further the camera is moved from the focus point. Beyond the focus point the light cone begins to diverge again and the same effect is seen if the camera is shifted away from the lens.

  Now, the Real World

In reality there are a number of factors which complicate this simple idea of focus. The first is that there are no ideal optical systems. All optics suffer from some sort of aberration. These aberrations are not necessarily manufacturing defects; all systems have some sort of image distortion even when perfectly designed and constructed. Newtonians, no matter how good, suffer from an aberration called coma. Ritchey-Chrétien telescopes all have inherent astigmatism. This is simply the nature of those particular designs.

A perfect optic, in theory, has no aberrations on axis. On axis means starlight coming straight through the center of the lens. However, every telescope has a certain field of view and can see objects off-axis, away from the center of the lens. Imagine a beam of light coming from a star which is slightly above the optical axis. The lens (even our ideal one shown above) focuses this light to a point below the on-axis focus point.

Above: Light from a star above the optical axis is focused to a location below the on-axis focal point.

This effect leads to an optical system having a focal plane, rather than a single focal point. This plane, ideally, would coincide with the CCD chip for perfect focus.

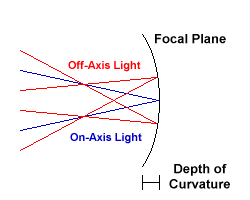
However, one characteristic (not really an aberration) of almost all telescope designs, is field curvature. Telescope lenses and mirrors are necessarily curved, and unless specially designed, the focal plane is curved as well. The curvature of the focal plane depends on the telescope design and focal ratio, but the most common designs all have a fair amount of field curvature.

Above: Off-axis light in a simplified lens is focused to points closer to the lens than on-axis light. The focal plane of this system is curved.

The potential problem here is that CCD chips are not curved. The curved focal plane means that certain areas of the image are focused and certain areas are not. This is not as much of a problem as it seems at first. The curvature is usually slight, and there other factors, as we'll see below, which help to minimize this problem.

Above: A curved focal plane does not perfectly coincide with the flat CCD chip.

  Depth of Focus

Let's, for a moment, go back to the simplified focal point idea. If a telescope focused starlight to a perfect point, the focus point would have a precise location, and there would be an exact point of focus. Moving the CCD chip even a millionth of an inch closer to or further from the lens would take the image slightly out of focus. Fortunately, in a real telescope system, there is a range of best focus.

Due to diffraction, a telescope does not focus starlight to a perfect point, but rather creates an image with a certain size. In theory, this size is dependent on the aperture of the telescope, meaning the star image is diffraction limited. A 4-inch telescope has a resolution (diffraction limit) of about 1.4 arcseconds. The resolution is also a function of wavelength, so this is an average which actually varies plus or minus about 25% from red light to blue light. We'll see in a second that it really doesn't matter much anyway. An 8-inch telescope has a theoretical resolution of about 0.7 arcsec, a 20-inch scope about 0.3 arcsec, and so on.

However, as mentioned in the Pixel Resolution Theory section, the real limitation during long exposures is much more likely to be the atmospheric stability, or seeing conditions. Typically, the resolution of a long-exposure CCD image is limited to about 2 arcsec, and values of 3-4 arcsec are by no means uncommon. Few locations have better seeing than this, even if they are exceptionally dark sites. Dark skies and stable skies are not necessarily the same thing, and in fact they are more often mutually exclusive.

This offers an advantage, however, when it comes to focusing. It means that focus is slightly less critical than it would otherwise be. The following example will show why.

  How Accurate Do You Need to Be?

Suppose you have an 8" f/10 Schmidt-Cassegrain telescope which you wish to focus accurately for CCD imaging. What is the range of focus (or depth of focus) tolerance on this telescope? Start by imagining the converging light cone again. If we assume the resolution of the telescope is 0.7 arcsec, there is a point just before reaching perfect focus where the converging light cone reaches this diameter. As the light begins to diverge again beyond the focus point, there is a certain distance from focus where the light cone is again 0.7 arcsec wide. Since the telescope cannot resolve anything finer than this size, if the CCD is placed anywhere within this range it will be accurately focused.

Above: At point A the converging light cone is 0.7 arcsec wide. At point B, the diverging cone grows again to 0.7 arcsec. The depth of focus is the range from point A to point B.

Now, in reality, the resolution will be more like 2 arcseconds due to seeing conditions and tracking errors. Since the light cone reaches the 2 arcsec width farther from each side of perfect focus, the depth of field is greater than if the telescope's optics alone were the limiting factor.

Above: If the resolution is 2", point A and point B are farther apart and the depth of focus is greater.

  In Practical Terms

Now it is possible to determine actual depths of focus for certain telescopes. Depth of focus is a function only of focal ratio. Why? Resolution is a function of diameter, so, for example, an 8-inch scope has a diffraction-limited angular resolution (Airy disk size) of 0.7 arcsec. A 4-inch telescope has an Airy disk size of 1.4 arcsec. If the 8-inch and 4-inch scopes both have the same focal ratio (say, f/10) then the 8-inch has twice the focal length (2000mm) and therefore twice the image scale. With twice the image scale and half the Airy disk size, the 8-inch will produce the samephysical Airy disk diameter at the focal plane as the 4-inch, as long as the focal ratio is equal.

Above: Depth of focus is greater for a slower focal ratio telescope (left). Since the light cone converges at a shallower angle, the distance from exact focus to the points on either side where the cone is a given width is larger than for a fast-focal-ratio scope (right).

The depth of focus for certain telescopes can be found on the chart below. The important thing is not the exact size of the depth of focus for a given scope, but rather the fact that the depth of focus is terrifyingly small for all scopes! Diffraction-limited depth of focus is less than 1/3 of a millimeter for an f/10 scope. This gives you an idea of how critical focus can be.

Focal Ratio	Depth of Focus (diffraction limited)
f/2	12 microns
f/3	26 microns
f/4	48 microns
f/5	72 microns
f/6	104 microns
f/7	141 microns
f/8	184 microns
f/9	233 microns
f/10	287 microns

  Back to the Curvature

The depth of focus on an 8" f/10 SCT telescope is 287 microns. The curved focal plane of a telescope has a certain depth, from the center of the curve to the edge of the curve. This depth is dependent on the width of the field of view--the width of the CCD chip--and the radius of curvature of the focal plane, which is an inherent function of a given telescope design.

Above: The depth of curvature for a curved focal plane.

If the depth of curvature over the width of the CCD chip is less than the depth of focus, the entire CCD chip can be in focus. If the depth of curvature is greater than the depth of focus, only a portion of the CCD can be focused. In this case, typically the central portion of the chip is in focus and the edges will be slightly out of focus.

Assuming the use of a typical APS-format CCD chip, which has a 27mm diagonal, the depth of curvature for this scope is 593 microns. Since the depth of focus is less than the curvature of field, the entire CCD chip cannot be in focus at once.

Above: On the left, the depth of curvature is less than depth of focus, and the entire chip would be in focus. On the right, the depth of curvature is greater than the depth of focus, and parts of the CCD would not be in focus.

Note: Even if the entire CCD chip is within the range of focus, there may still be other aberrations (coma, astigmatism, etc.) which prevent stars from appearing perfectly sharp across the entire field.

Schmidt-Cassegrains and Ritchey-Chretiens tend to have about as much field curvature as you are likely to find in any amateur telescopes. While a 15mm chip may be in focus across the entire field, a 35mm chip (which has a 42mm diagonal size) requires a depth of focus of 1440 microns on an 8" f/10 telescope. Since the depth of focus on an f/10 scope is only 287 microns, the entire CCD cannot be in focus at once. However, remember that this is for diffraction-limited focus. If we let the focus be seeing-limited (2 arcsec rather than 0.7 arcsec), the depth of focus increases to 786 microns, enough to get a 31mm sensor in focus.

If we assume that when focus is achieved, the area of the CCD used to focus will be in the center of the depth of focus, it can be shown that the center of the CCD should not be used to focus. The curved field of most scopes will be convex toward the aperture (as shown in the diagrams above). If the depth of curvature is 605 microns (as it would be for a 35mm-format CCD on a 12.5" f/9 Ritchey-Chretien), and the center of the field coincides with the center of the depth of focus, the outer edges of the chips will extend out of the range of good focus (which is 233 microns in depth). By placing the star to be focused about halfway out to the edge of the chip, it is more likely that the entire CCD will end up within the range of focus. Note that this is much less critical on a scope with a flatter field, or when using a smaller CCD chip.

Above: This diagram shows the depth of focus and the field curvature for a 12.5" f/9 Ritchey-Chretien, as described above. When the CCD is focused using the center of the field, only an 18.4mm circular area of the CCD will be in focus; the rest of the curved focal plane is outside the depth of focus. This diagram is exaggerated 5x in the horizontal direction to clearly show the curvature and depth of focus.

Above: When an off-axis area of the CCD is used to focus, more of the curved focal plane falls within the depth of focus and a larger area of the CCD will be in focus.

Above: A comparison of the area of a full-frame 35mm-format CCD that would be in focus using the methods above.